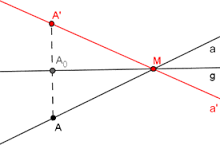
}1.Определение:Преобразувание в равнината, при което на произволна точка Х се съпоставя симетричната й точка Х\' относно дадена права g, се нарича осева симетрия.

Теорема: Всяка осева симетрия е еднаквост. 

Тъй като осевата симетрия е еднаквост, тя притежава всички свойства на еднавостите. 

Образът на права намираме, като построим образите на две произволни точки от нея. 

Образът на триъгълник намираме, като построим образите на върховете му. 

Образът на окръжност намираме, като построим образът на центъра й.

Правоъгълникът има две оси на симетрия - правите на двете му средни отсечки. 

Квадратът има четири оси на симетрия - правите на двете му средни отсечки и диагоналите му. 

Един триъгълник има ос на симетрия тогава и само тогава, когато е равнобедрен - и това е симетралата на основата. Равностранният триъгълник има три оси на симетрия. 

Правата на всеки диаметър на една окръжност е нейна ос на симетрия. 

Знаете ли, че осевата симетрия се нарича и огледална симетрия? Това е така, защото образите на обектите при нея са като отражение в огледало. Искате ли да станете добри в построяването на образи на точка, права, отсечка и геометрична фигура при осева симетрия? Да откривате кои са осите на симетрия на различните фигури и други обекти в природата и в живота? Онлайн упражнението по математика за 8. клас "Осева симетрия. Всичко най-важно" ще ви помогне да го направите. Приятно пътуване в огледалния свят на задачите за осева симетрия!

1зад:Точката X' е образ на X при осева симетрия. Постройте образа на произволна точка Y при същата симетрия.

2зад:Докажете, че правоъгълника е симетрична фигура с оси на симетрията правите, съединяващи средите на срещуположните страни.

3зад:Докажете, че ромбът е симетрична фигура с оси на симетрия всеки от диагоналите му.

4зад:Докажете, че ако един трапец е симетрична фигура, то той е равнобедрен.